PERFORMANCE¶
Warning
Scalability tests reported below have been run with an old AMITEX_FFTP version and an old HPC machine
Main conclusions are not expected to be modified with more recent versions
The following scalability performances have been evaluated with the 1.0.1 version and the poincare IBM cluster available at Maison de la Simulation which consists of 92 nodes with 2 processors Sandy Bridge E5-2670 and 32Go of RAM per node.
All the simulations have been performed with default algorithm parameters (Basic Scheme + Convergence Acceleration procedure, Filtered discrete Green operator with the hexaedral filter).
Scalability tests are evaluated from 16 to 1024 cores (1 to 64 nodes).
As shown below, the scalability strongly depends on the numerical efficiency of the behavior law evaluation.
MAIN CONCLUSIONS:
- for “heavy” behaviors : Strong and weak scalabilities are quasi-ideal.The parallel implementation is very efficient to reduce elapsed time and increase the problem size.
- for “light” behaviors : Strong and weak scalabilities are less good. However, the parallel implementation is quite efficient to increase the problem size and can be efficient to reduce the elapsed time if the problem size is large enough.
Note that AMITEX_FFTP is rather developed to account for “heavy” behaviors, accounting for more and more complex physical mechanisms, than simple linear elasticity.
Scalability with “numerically heavy” behaviors (e.g. cristalline plasticity)¶
As shown on the figures below, all the unit-cells used for the following studies consist of periodic multiplications of a reference \(128^3\) unit-cell (polycrystal). The behavior is a cristalline behavior available within the Mfront library (see Installation).
|
|
|
| 1 cell (128^3) | 8 cells (256^3) | 64 cells (512^3) |
| Examples of unit-cells used for weak and/or strong scalability studies | ||
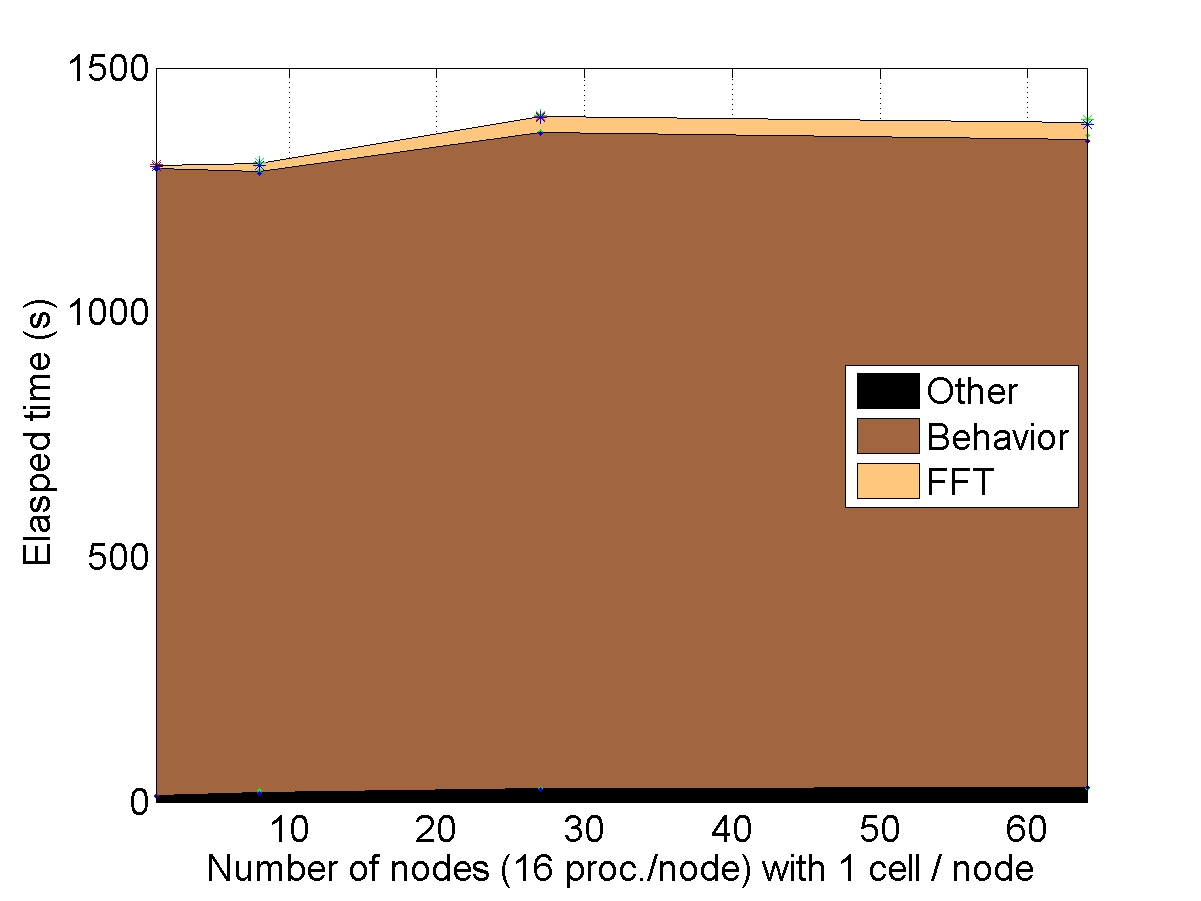
WEAK SCALABILITY: N cells on N nodes
The number of cells within the unit-cell is equal to the number of nodes used for the simulation.
CONCLUSION : with “heavy” behaviors, the AMITEX_FFTP parallel implementation is very efficient to increase the problem size (quasi-ideal weak scalability)
- Compared to the behavior law, the evaluation of FFTs that involves MPI communications is a small part of the elapsed time,
- As the evaluation of the behavior law is local, it is very efficiently distributed and the elasped time is almost constant and the weak scalability quasi-ideal.
|
| N cells on N nodes |
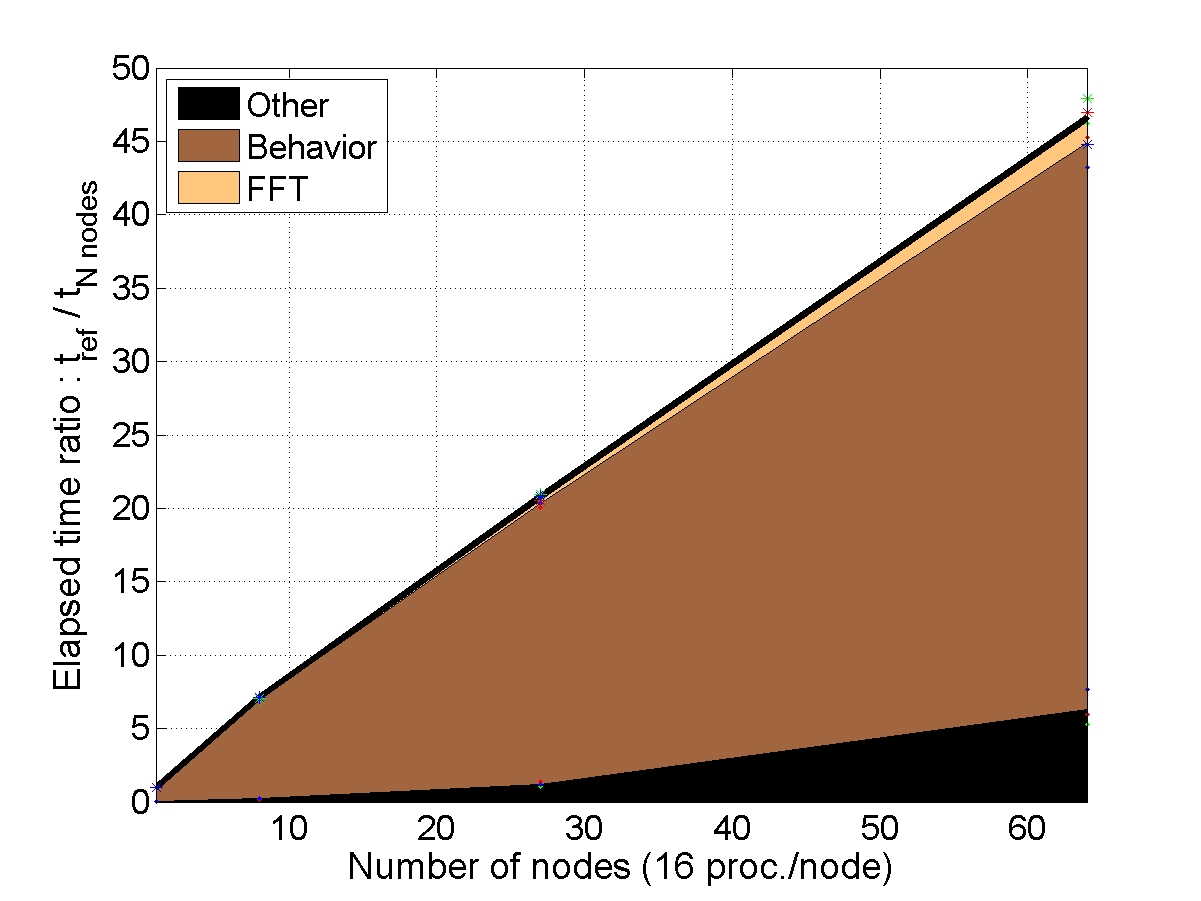
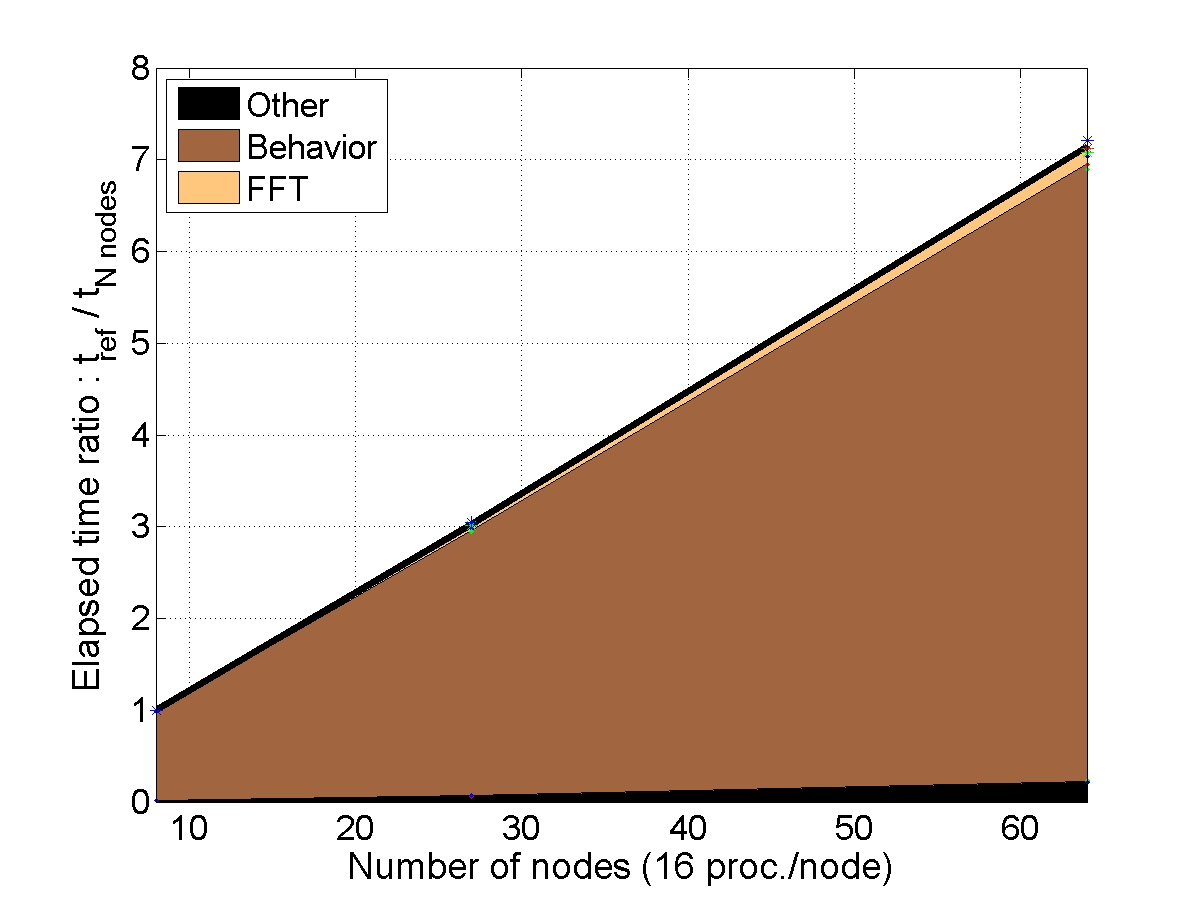
STRONG SCALABILITY: X cells on N nodes
The number of cells within the unit-cell is fixed (1 or 8) and the number of nodes used for the simulation increases. The elapsed time is compared to a reference elapsed time on 1 node (or 8 nodes for the bigger unit-cell).
CONCLUSION : with “heavy” behaviors, the AMITEX_FFTP parallel implementation is very efficient to decrease the elapsed time (very good strong scalability)
- Compared to the behavior law, the evaluation of FFTs that involves MPI communications is a small part of the elapsed time,
- As the evaluation of the behavior law is local, it is very efficiently distributed and the elapsed time decreases significantly with the number of nodes and the strong scalability is very good (the elapsed time ratio is ~45 instead of 64, for 64 nodes used instead of 1)
- Note that the use of the 2decomp library and a 2D decomposition allows to use more than 128 and 256 processors (8 and 16 nodes) imposed by 1D decompositions for the two problem sizes studied below (\(128^3\) and \(256^3\)),
- in the example below, the 8-cell problem (\(256^3\)) is too large to be simulated on 1 node and the reference simulation is evaluated on 8 nodes, the elapsed time ratio is almost ideal (7.2 instead of 8, for 64 nodes instead of 8).
|
|
|
|
Scalability with “numerically light” behaviors (e.g. linear elasticity)¶
As shown on the figures below, all the unit-cells used for the following studies consist of periodic multiplications of a reference \(128^3\) unit-cell (polycrystal). Matrix is stiffer than inclusions with an elastic contrast of 100.
|
|
|
|
| 1 cell (128^3) | 8 cells (256^3) | 64 cells (512^3) | 512 cells (1024^3) |
| Examples of unit-cells used for weak and/or strong scalability studies | |||
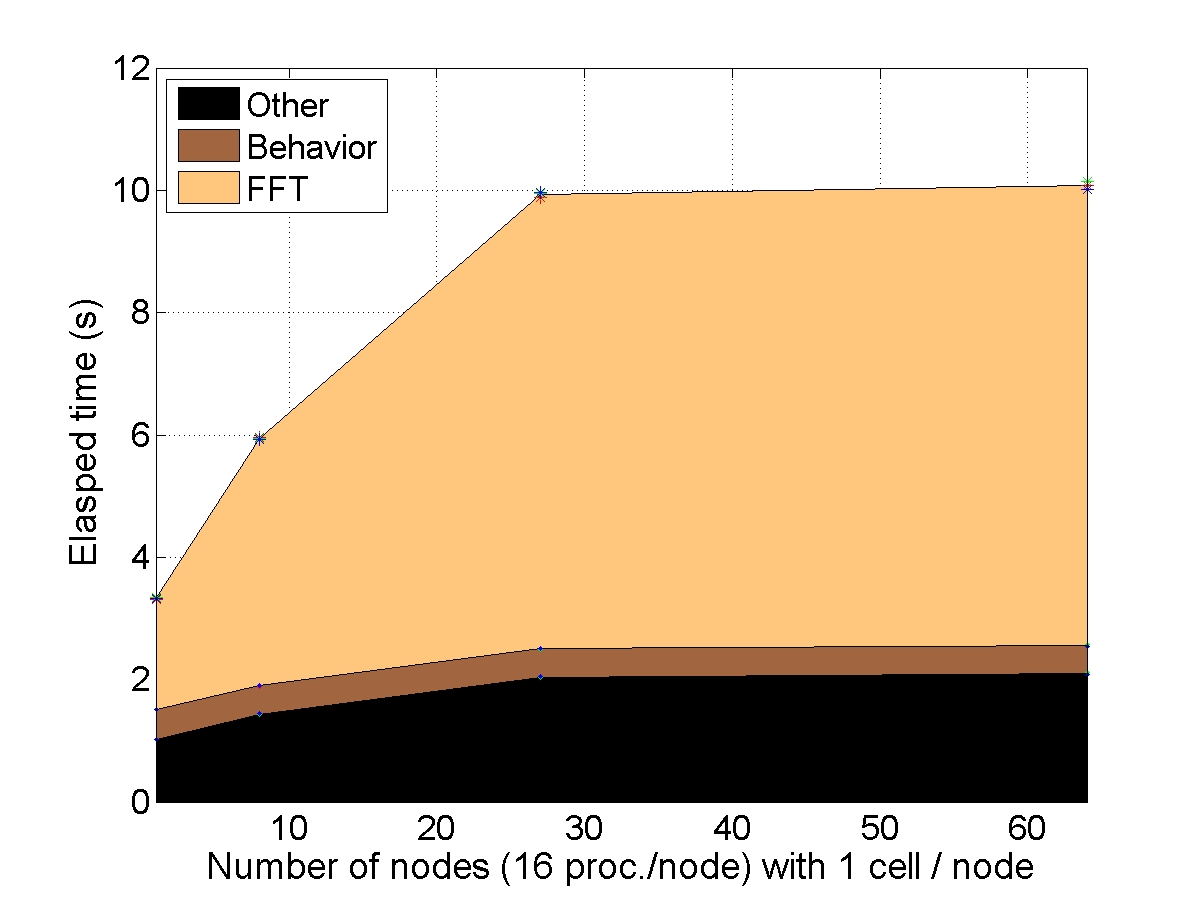
WEAK SCALABILITY: NxX cells on N nodes
The number of cells within the unit-cell is proportional (x1 or x8) to the number of nodes used for the simulation.
CONCLUSION : with “light” behaviors, the AMITEX_FFTP parallel implementation can be used quite efficiently to increase the problem size (weak scalability)
- Compared to the behavior law, the evaluation of FFTs that involves MPI communications is an important part of the elapsed time,
- If not ideally scalable, the elapsed time appears to be quite stable above 27 nodes,
- The elapsed time ratio is improved when the problem size/node increases (~3 for Nx1 cells simulations and ~2 for Nx8 cells simulations)
|
|
| (Nx1) cells on N nodes | (Nx8) cells on N nodes |
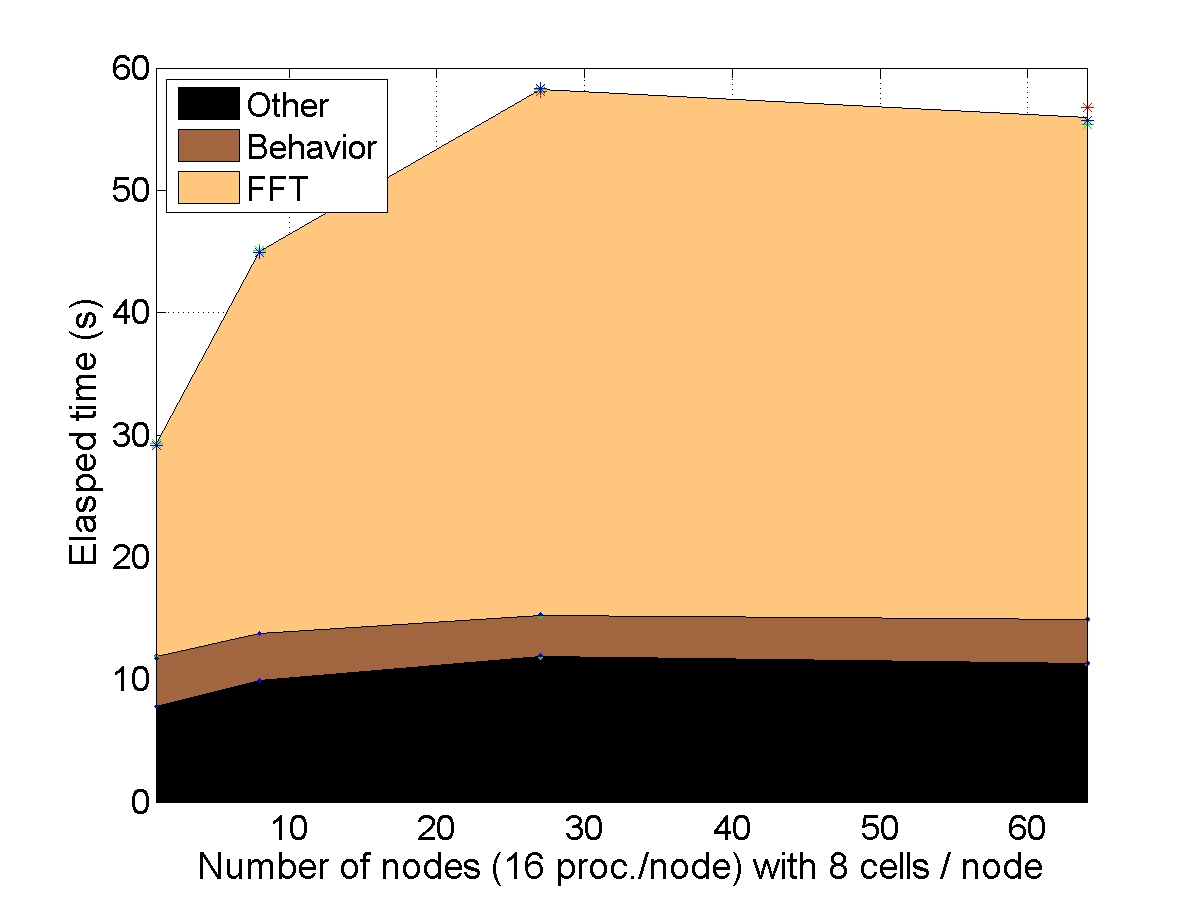
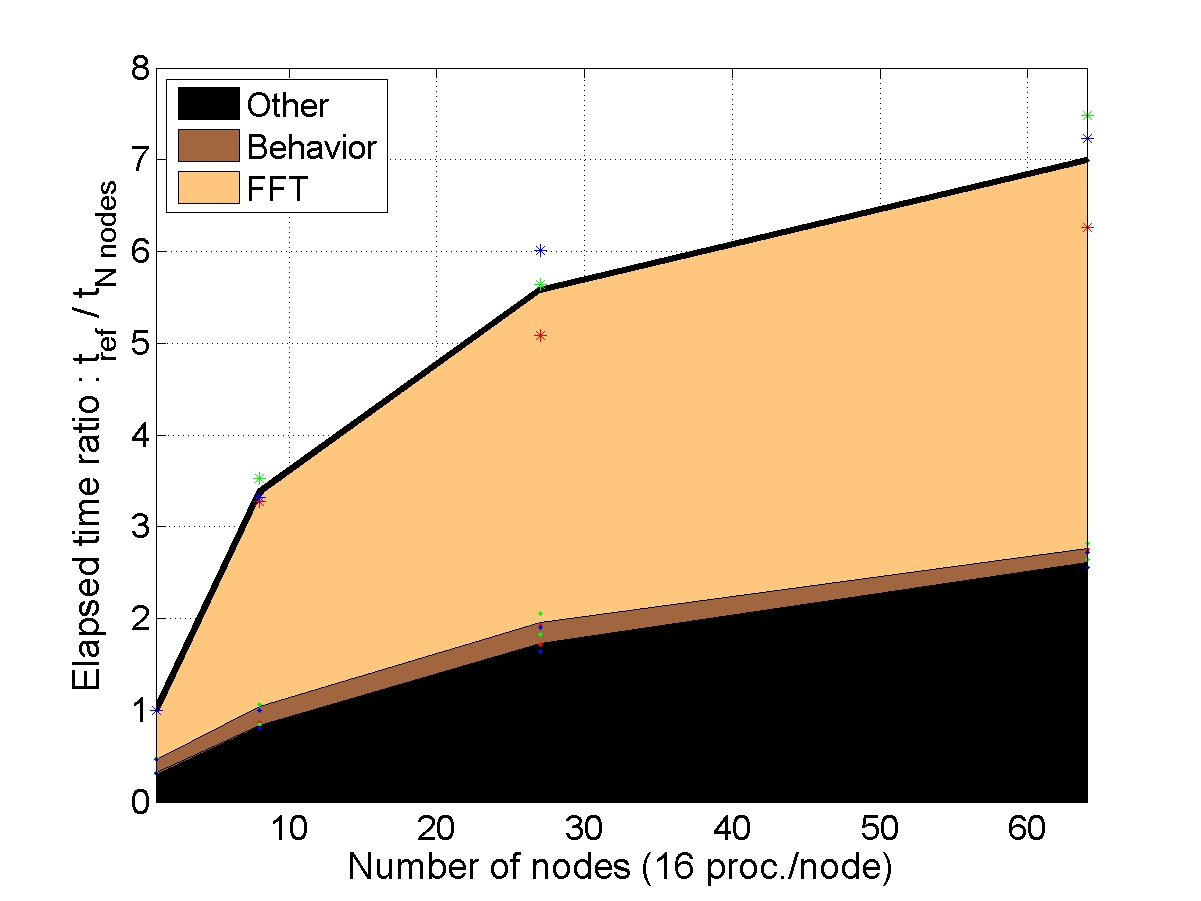
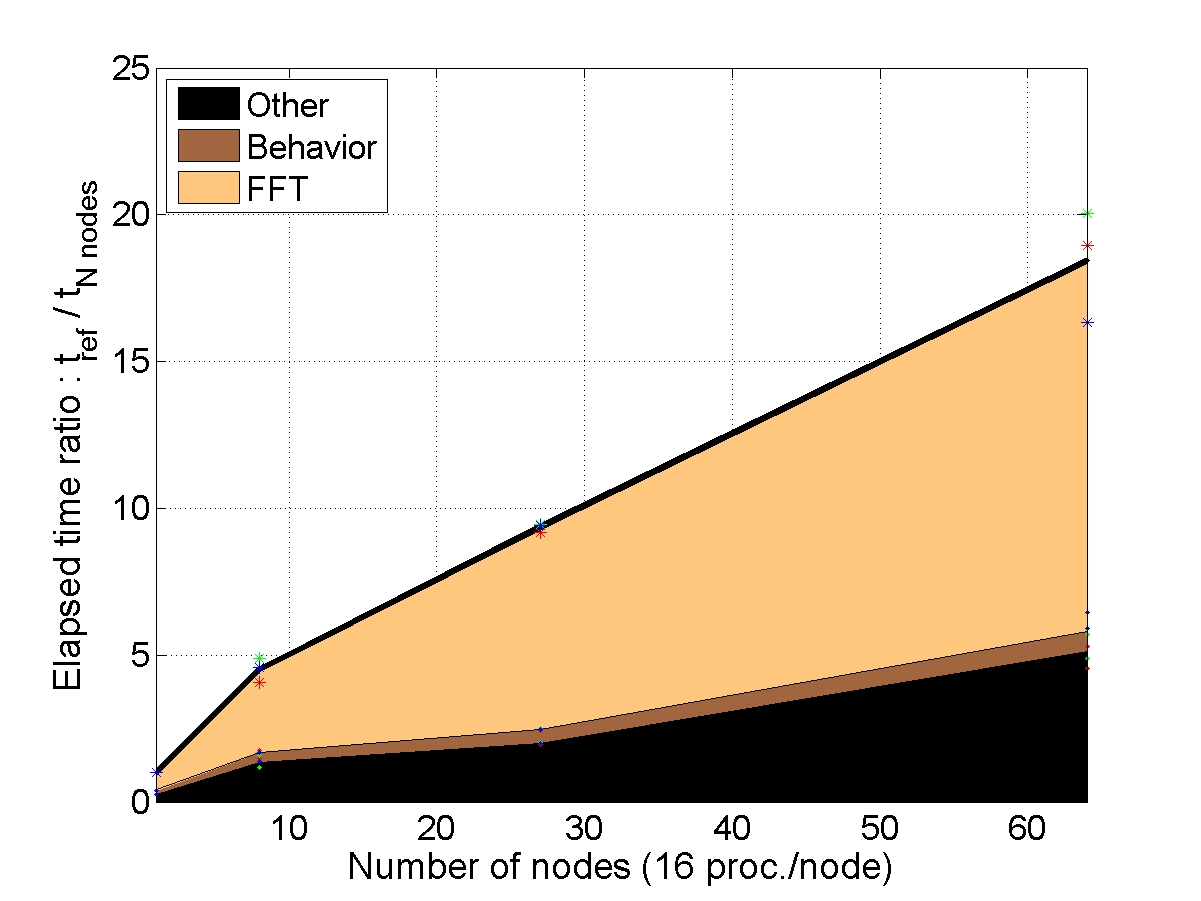
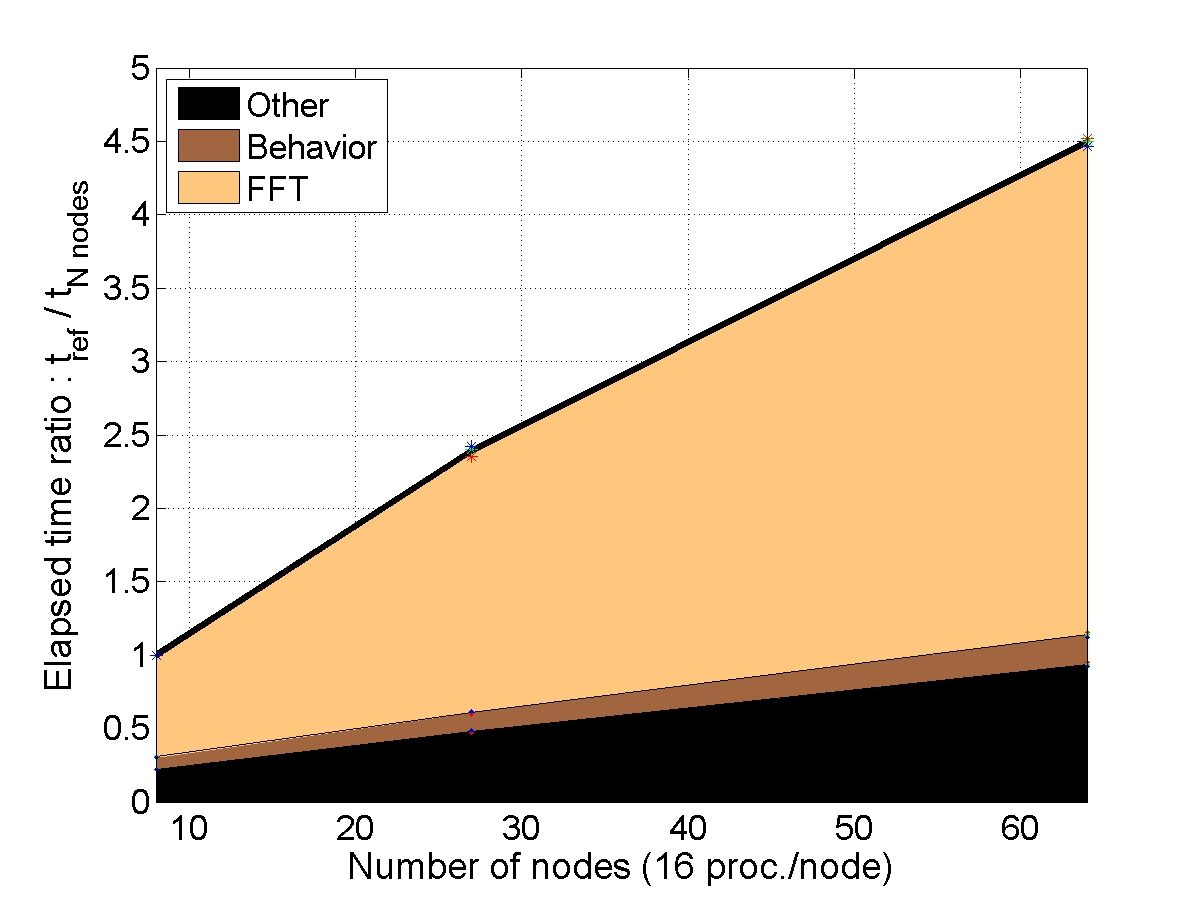
STRONG SCALABILITY: X cells on N nodes
The number of cells within the unit-cell is fixed (1, 8 or 64) and the number of nodes used for the simulation increases. The elapsed time is compared to a reference elapsed time on 1 (or 8 nodes for the bigger unit-cell).
CONCLUSION : with “light” behaviors, the AMITEX_FFTP parallel implementation is efficient to reduce the elapsed time if the problem size is large enough
- Compared to the behavior law, the evaluation of FFTs that involves MPI communications is an important part of the elapsed time,
- For small problems (\(128^3\)), the elapsed time ratio is far from the ideal when the number of nodes increases : ~7 instead of 64 (for 64 nodes instead of 1).
- For a bigger problem (\(256^3\)), the difference decreases: ~7 instead of 64 for 1024 proc.
- For a much bigger problem (\(512^3\)) which cannot be simulated on a single node, the elapsed time ratio (with a reference simulation on 8 nodes) is ~4.5 instead of 8 (64 nodes instead of 8).
- Simulations on more than 128, 256 or 512 processors (8, 16, or 32 nodes) for the problem sizes \(128^{3}, 256^3\) and \(512^3\) (respectively) are possible thanks to the 2D pencil decomposition provided by the 2decomp library.
|
|
|
|
|
|